Система счисления

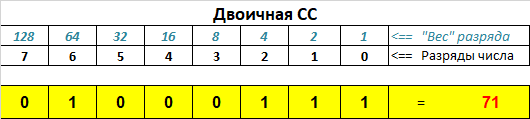
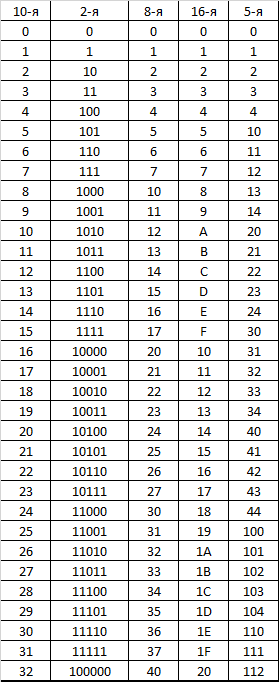
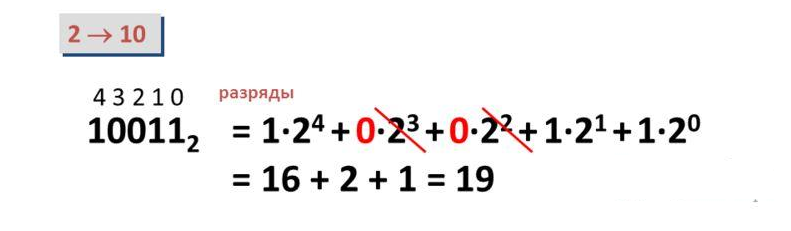Введение

Зачем нужны системы счисление. Объяснение смысла.SciencePub

Кодирование информации: процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки.
Система счисления: это способ записи количества предметов + правила выполнения арифметических дейсвий в данной СС.

Как только предметов, принадлежащих древнему человеку, стало много и их стало невозможно носить с собой - появилась потребность счета.

Еще в самые отдаленные времена людям приходилось считать различные предметы, с которыми они встречались в повседневной жизни. Вначале букв не было. Мысли и слова выражались при помощи рисунков на скалах, на стенах пещер, на камнях. Для запоминания чисел люди пользовались зарубками на деревьях и на палках и узлами на веревках. Это и была простейшая и самая древняя – так называемая, унарная система. В ней для записи любых чисел используется всего один символ – палочка, узелок, камушек. Используя именно эту систему счисления, вас научили считать (сами того не осознавая, этим кодом пользуются малыши, показывая на пальцах свой возраст).

Люди использовали разные способы записи чисел. Римляне применяли 7 знаков для семи цифр:

I	V	X	L	C	D	M
1	5	10	50	100	500	1000

При чтении числа они складывали цифры и получали результат

XXI это X + X + I = 21

MMXXIII это 1000 + 1000 + 10 + 10 + 1 + 1 + 1 = 2023

Если бы мы продолжали так записывать числа, то читали так:
356 = 3 + 5 + 6 = 14

Для записи цифр, отсутствующих в алфавите применялось правило 2-х цифр:

IX = 10 - 1 = 9

MCMXCIX = 1000 + (1000-100) + (100-10) + (10-1) = 1999

если перед большей цифрой стояла меньшая, то из большей нужно вычесть меньшую.

При таком способе записи вес (величина) цифры не зависит от его положения в записи числа.

Мы применяем другой способ записи
111 = 1*100 + 1*10 + 1*1
величина цифры зависит от ее расположения в записи числа – позиционная СС.

Не позиционная СС: вес цифры (количество чего-либо) НЕ зависит от положения цифры в записи числа
Позиционная СС: вес цифры (количество чего-либо) зависит от положения цифры в записи числа - ее разряда; мы используем в настоящее время
Разряд цифры: номер ее места в записи числа в позиционных СС

Позиционные системы СС

В начальной школе вас научили определять разряд числа:

Разряд единиц
Разряд десятков
Разряд сотен
Разряд тысяч
Разряд десятков тысяч и т.д.

Мы привыкли к тому, что соседние разряды по "цене" отличаются в 10 раз.

Мы знаем алгоритмы выполнения действий столбиком. Они универсальны и применяются во всех СС.

Число можно разложить в числовой ряд – представить в виде суммы цифр с указанием их величины:
1999 = 1*1000 + 9*100 + 9*10 + 9*1 = 1*10³ + 9*10² + 9*10¹ + 9*10⁰

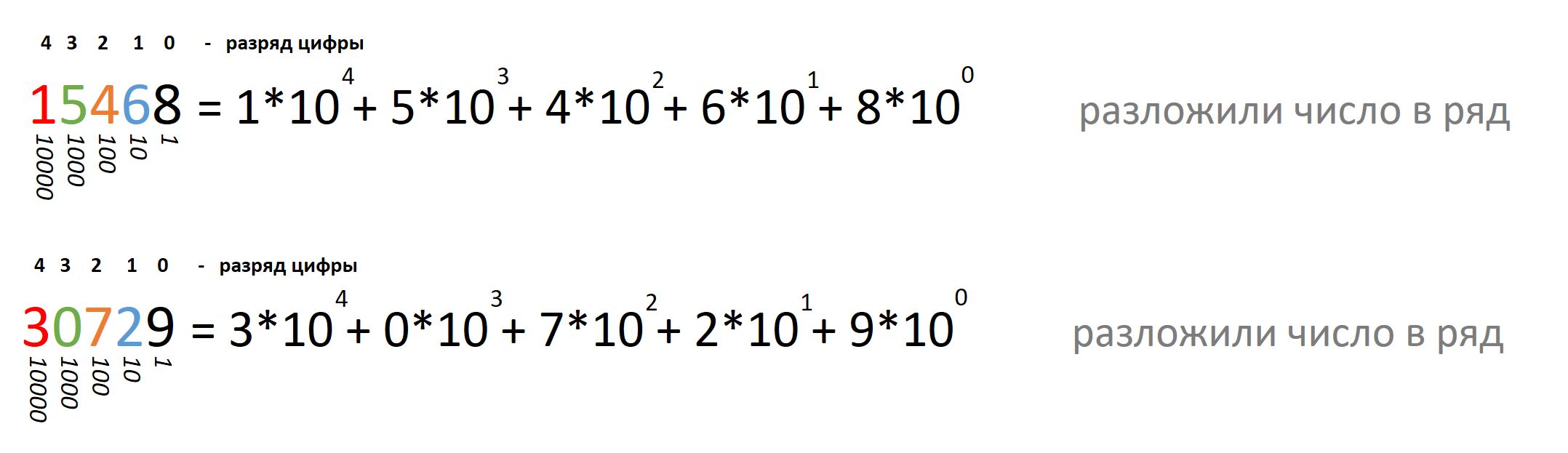
ПКМ - Открыть изображение в новой вкладке

Свойства СС:

Алфавит - набор символов для обозначения отдельных цифр
Основание СС - количество символов (закорючек, которые мы рисуем в тетради) в алфавите
Правила выполнения арифметических действий в данной СС

ПРИМЕРЫ СС

Кратко и понятно
• Из грязи - в князиСистемы Счисления
• СказкаТак появилось двоичное исчисление.

Число показывает количество чего-либо

Мы видим 5 десятков и 6 штук яблок = 56₁₀. Еще можно записать таким образом: 70₈, 111000₂, 38₁₆, 211₅, 2002₃, 62₉, ...

I. Десятичная СС - в ней мы все хорошо ориентируемся.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание = 10
Правила выполнения арифмитических действий: мы все знаем наизусть (7+8=15, 7*8=56, …)
Есть один нюанс - при выполнении арифметических действий появляется старший разряд:
7 + 2 = 9
7 + 3 = 10 - цифр старше 9 нет ⇛ повился разряд 10-ков.
Это характерно для всех СС и мы это будем учитывать в дальнейшем.

Однако цены соседних разрядов могут различаться не в 10 раз! Отголоски одного из способов сохранились в английском языке: есть названия цифры 11 (eleven) и 12 (twelve), значит у них было не 10, а 12 цифр!

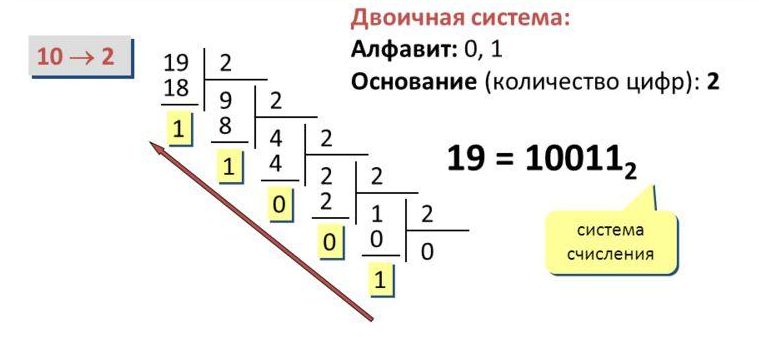
II. Двоичная СС

Смотрим мультики:
• Просто о двоичной системе счисления и двоичном коде. #1Правильное программирование
• Как на самом деле работает двоичный код? Conyr / Лазиз Ходжаев

Алфавит: 0, 1
Основание = 2
Правила выполнения арифмитических действий:
1 + 0 = 1
1 + 1 = 10 - это не десять! - цифр старше 1 нет ⇛ появился разряд двоек: 1 двойка и 0 единиц

В двоичной системе цена разряда цифры в записи числа:

Разряд единиц
Разряд двоек
Разряд четверок
Разряд восьмерок
Разряд шестнадцаток и т.д.

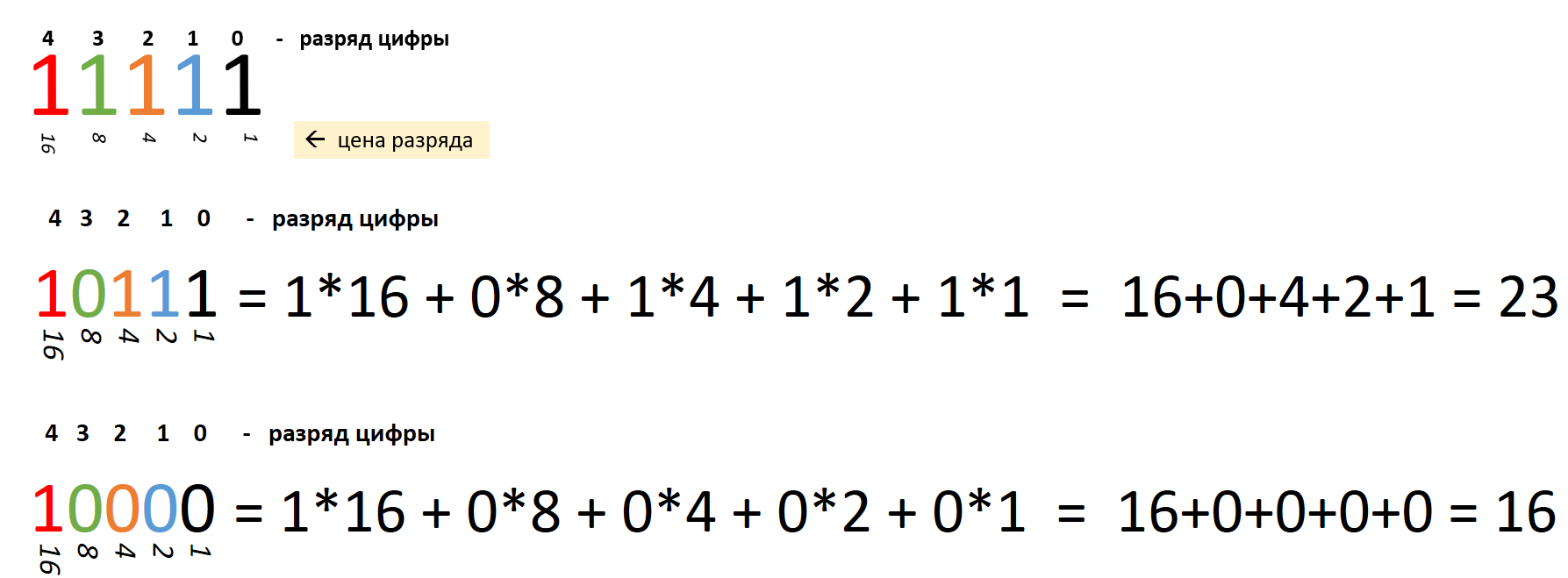
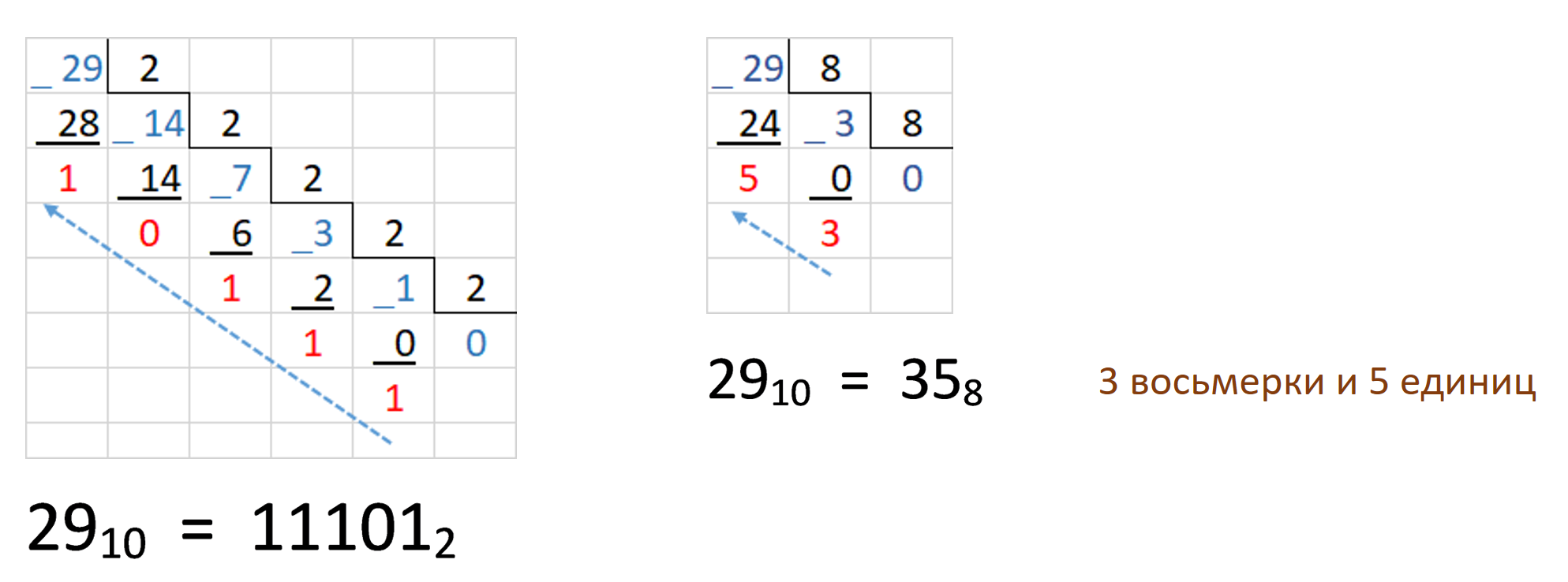
III. Восьмеричная СС

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
Основание = 8
Правила выполнения арифмитических действий:
1 + 6 = 7
7 + 1 = 10 - цифр старше 7 нет ⇛ появился разряд восьмерок: 1 восьмерка и 0 единиц

В восьмеричной системе цена разряда цифры в записи числа:

Разряд единиц
Разряд восьмерок
Разряд 64
Разряд 512
Разряд 4096 и т.д.

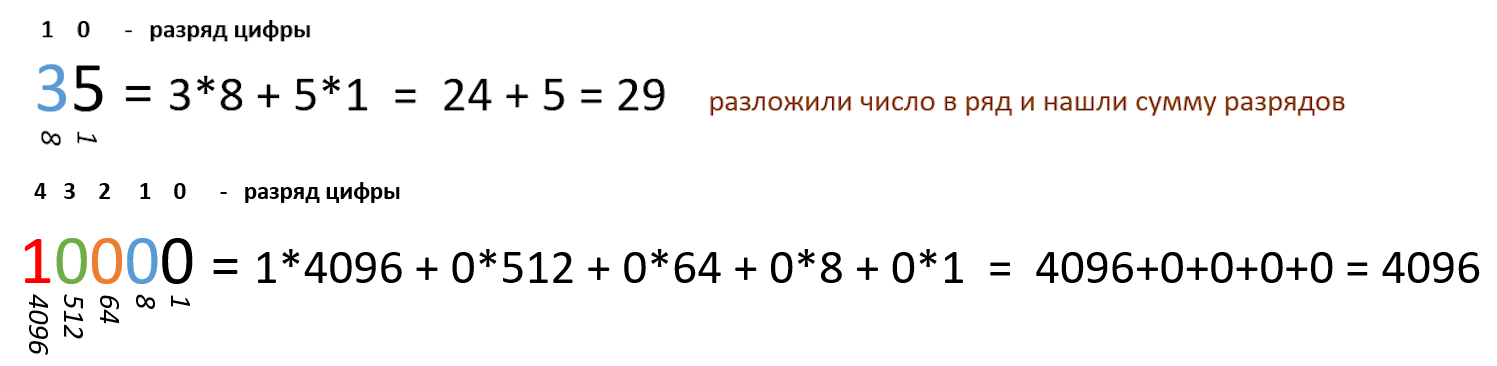
IV. Шестнадцатеричная СС

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F - появилась непривычная(!) запись недостающих цифр 😓
где A = 10, B = 11, C = 12, D = 13, E = 14, F = 15
Основание = 16
Правила выполнения арифмитических действий:
8 + 1 = 9
9 + 1 = A - это десять для нас
A + 1 = B
B + 1 = C
C + 1 = D
D + 1 = E
E + 1 = F
F + 1 = 10 - цифр старше F нет ⇛ появился разряд 16: 1 шестнадцатка и 0 единиц
10 + 1 = 11 - 1 шестнадцатка и 1 единица

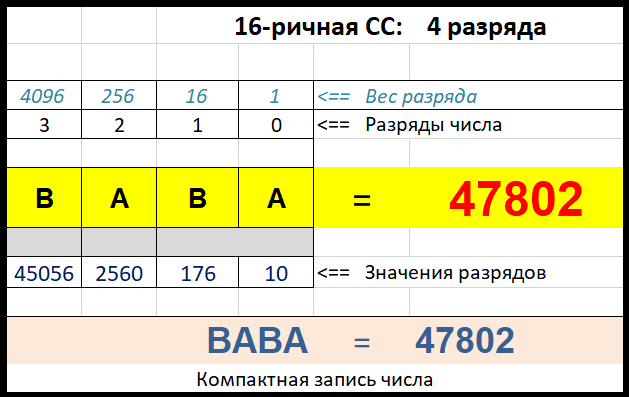
В 16-ричной СС цена разряда цифры в записи числа:

Разряд единиц
Разряд шестнадцаток
Разряд 256
Разряд 4096
Разряд 65 536 и т.д.

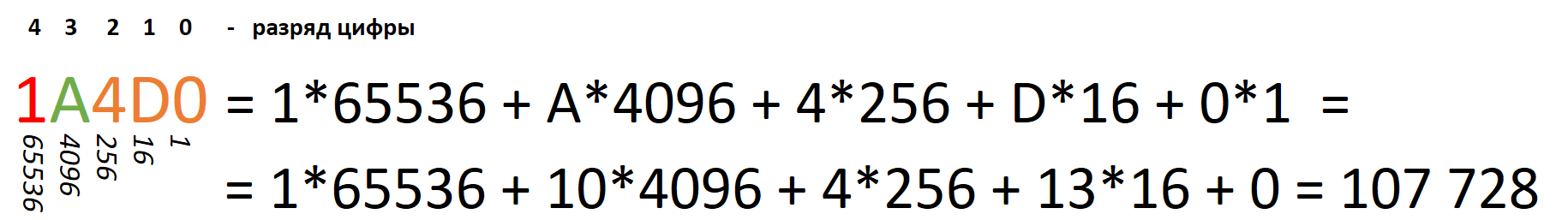
Важно! При записи текста на разных языках мы ориентируемся на начертания букв. И хорошо понимаем на каком языке написан текст.
При записи количества в разных СС используют одни и те же символы (цифры). Поэтому применяют _{нижние индексы} для различия разных способов ("разных языков") записи чисел: 1234_N, где N - онование СС.
Здесь написаны числа, указывающие разное количество: 1234₈, 1234₁₆, 1234₅, 1234₉, 1234₇, 1234₂. Одна из записей неверна - какая и почему? Какое из этих чисел является наименьшим?
На самое большое количество указывает запись 1234₁₆. Разряды "дорожают" в 16 раз. В привычной нам 10-й СС всего в 10 раз.
Еще пример. Дано 2 числа: 1010₂, 1010₁₀.
1010₂ = 10 (десять), а второе 1010₁₀ - одна тысяча десять. Чувствуете разницу?

Двоичная арифметика

Загадка 😔

**10110₂ + 100001₂ = ?₂ 10110₂ * 100001₂ = ?₂**

Разгадка

Как одно и тоже количество записать в разных СС?

Начнем с самого непривычного:
ABBA₁₆ = A*16³ + B*16² + B*16¹ + A*16⁰ =
= 10*16³ + 11*16² + 11*16¹ + 10*16⁰ = 43962₁₀

Еще примеры
2023₈ = 2*8³ + 0*8² + 2*8¹ + 3*8⁰ = 2*512 + 0*64 + 2*8 + 3*1 = 1043₁₀

Алгоритм перевода из других СС в 10-ную СС:

Написать над цифрами номера разрядов, начиная с 0, справа-налево.
Найти сумму разрядов каждой цифры числа. Для этого цифру умножаем на "вес" соответствующего разряда (смотри пример с АВВА).
И записать ответ в тетради.

Чтобы перевести число, скажем, 12345_N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5_N = 1·N⁴ + 2·N³ + 3·N² + 4·N¹ + 5·N⁰ , где N⁰ = 1.

Скачайте файл

Кратко и понятно. Из грязи - в князи:
• Применение двоичной системы счисления в реальной жизни.Про OR-cod
• Применение восьмиричной системы счисления и права доступа к файлу.
• Применение шестнадцатеричной системы счисления в реальной жизни Про фильмМАРСИАНИН

Алгоритмы записи чисел в "непривычных" СС.

Вариант 1, основной.

Для перевода из 10-й СС в другие делим число (а потом частное) на новое основание с остатком, пока частное не станет = 0.
Переписываем остатки , начиная с последнего. Это и будет ответ

Вариант 2, для небольщих чисел

В тетради черкаемся, можно не так красиво:

Ставим горизонтально несколько точек (вместо 0)
Нумеруем разряды справа налево
Указываем цену каждого разряда в данной СС
Подбираем слагаемые для получения нужного числа
Любуемся полученным результатом
8-я СС 3 2 1 0 • 1 0 7 = 71 512 64 8 1

Скачиваем (xlsx) и учимся

Еще алгоритмы...

Есть алгоритмы перевода чисел из 2-й СС в СС с основанием, кратным 2ⁿ, где n = 1, 2, 3, 4, …

АЛГОРИТМЫ

I. Из 2-й - в 8-ю (или 16-ю) систему счета

Разбить число на группы цифр по 3 (или 4) справа налево
Если в последней группе слева не хватает цифр – добавить впереди 0
Записать каждую группу одной цифрой в новой СС (это ответ)

Пример: Из 2-й - в 8-ю

11111000001011010110111₂ = ?₈ = 37013267₈

Разбиваем на группы по 3 цифры справа налево, дописываем слева недостающий 0
011 111 000 001 011 010 110 111 3 7 0 1 3 2 5 7 - это ответ

Пример: Из 2-й - в 16-ю

11111000001011010110111₂ = ?₁₆ = 7C16B7₁₆

Разбиваем на группы по 4 цифры, дописываем слева недостающий 0
0111 1100 0001 0110 1011 0111 7 C 1 6 B 7 - ответ

II. Из 8 (или 16) - в 2-ю систему счета

Из 8: записать каждую цифру группой из 3 цифр в 2-й СС (это ответ)
Из 16: записать каждую цифру группой из 4 цифр в 2-й СС

Пример: Из 8-й - в 2-ю

3051₈ = ?₂ = 11000101001₂

Каждую цифру числа заменяем группой из 3 цифр в 2-й СС. Впереди стоящий 0 отбрасываем.
3 0 5 1 011 000 101 001 - ответ

Пример: Из 16-й - в 2-ю

A0F921₁₆ = ?₂ = 101000001111100100100001₂

Каждую цифру числа заменяем группой из 4 цифр в 2-й СС. Впереди стоящий 0 отбрасываем.
A 0 F 9 2 1 1010 0000 1111 1001 0010 0001 - ответ

Шпаргалка

Системы счета (СС)