Введение в мир множеств

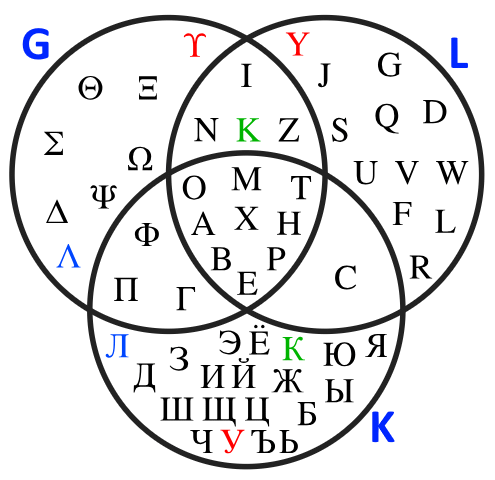
Сколько различных множеств вы видите?

Множество

совокупность объектов произвольной природы, которая рассматривается как единое целое

Введем некоторые обозначения.

Множества принято обозначать прописными буквами латинского алфавита (A, B, C, …).

• M = {1, 3, 5, 7, 9} множество однозначных нечетных чисел
• A = {x | 10 ≤ x ≤ 99} множество целых двузначных чисел
• B = {0, 1} цифры двоичного алфавита
• C = {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} гласные буквы русского алфавита

Объекты, входящие в состав множества, называются его элементами и обозначаются строчными латинскими буквами.

• x ∈ M - x элемент множества M (x принадлежит множеству M)
• x ∉ M - x не является элементом множества М (x не принадлежит M)
• |M| или N_м - мощность (количество элементов) множества М
• ∅ - пустое множество – множество, в котором нет ни одного элемента

Мощностью конечного множества называется число его элементов. Мощность множества X обозначается |X| или N_X

Примеры.

• |∅| = 0 или N_∅ = 0 - пустое множество
• |А| = 33 или N_A = 33 - множество букв русского алфавита
• |В| = 4 или N_B = 4 - В = {зима, весна, лето, осень} множество времен года

Способы задания множеств:

1. Перечислением элементов
   • Пример. Множество букв в слове ГИГАБАЙТ обозначим Х и зададим его перечислением: Х = {А, Б, Г, И, Й, Т}. Мощность |А| = 6
   • Способ задания множества перечислением его элементов не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем. Например, невозможно перечислить множество рыб в Тихом океане, хотя совершенно очевидно, что их число конечно.
2. Описание элементов определяющим свойством: A = {a | свойства элементов множества A}.
   Более формально A = { x | P(x) }, которую читают следующим образом: "A есть множество элементов x таких, что для них выполняется свойство P(x)".
   • B = { x| x- натуральное число, меньшее 10 } при этом, очевидно, B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.
   • E = { x| x = 3^k, k - любое нартуральное число}.
     Это бесконечное множество степеней числа 3.
     E = {3, 9, 27, 81, 243, 729, 2187, 6561, ...}

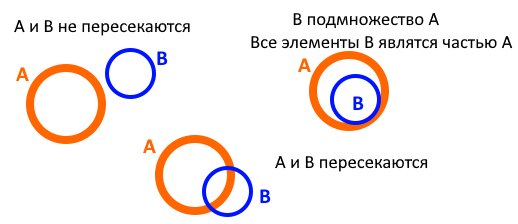
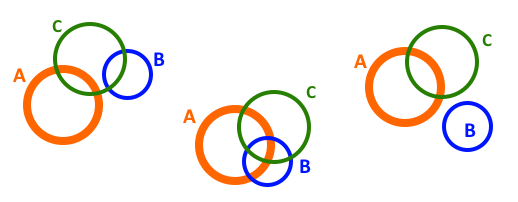
Операции над множествами

Слева общие элеметы множеств X и Y - ПЕРЕСЕЧЕНИЕ множеств
Справа ВСЕ элементы обоих множеств - ОБЪЕДИНЕНИЕ множеств
Обратите внимание на выделенные цветом числа на рисунке выше.
5 + 4 = 2 + 7
|X| + |Y| = |X ∪ Y| + |X ∩ Y|
(запишите в тетради формулу с пояснениями)

Смотрим (с паузами и конспектом изучаемой темы в тетрадь)

Отличный сериал! Кликаем справа 'Из той же серии' → конспект

Пересечение и объединение множеств

Теория множеств для начинающих

Диаграммы Эйлера-Венна

Диаграмма Венна (Эйлера — Венна)

схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) множеств.

Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные).

|G| = 24 греческий, |L| = 26 латиница, |K| = 33 кириллица
|G∪L∪K| = |G| + |L| + |K| - |G∩L| - |G∩K| - |L∩K| + |G∩L∩K|
|G∩L∩K| = |G| + |L| + |K| - |G∪L| - |G∪K| - |L∪K| + |G∪L∪K|

Решение задач на множества с помощью кругов Эйлера. Marianna L

Понятное и подробное объяснение! Кафедра математики. On-line

Круги Эйлера. Решение задач на поиск информации в Интернет. Юлия Шелякина

Выводы

Формула включения-исключения (англ. Inclusion-exclusion principle)

комбинаторная формула, выражающая мощность объединения конечных множеств через мощности всех множеств и мощности всех их возможных пересечений.

Для двух множеств X и Y формула включения-исключения
|X| + |Y| = |X ∪ Y| + |X ∩ Y|

Для трех множеств А, В и С формулы включений-исключений
|A∪B∪C| = |A| + |B| + |C| - |A∩B| - |A∩C| - |B∩C| + |A∩B∩C|
|A∩B∩C| = |A| + |B| + |C| - |A∪B| - |A∪C| - |B∪C| + |A∪B∪C|

При записи поисковых запросов в интернете обычно применяют другие сиволы пересечения, объединения, ...
X + Y = X|Y + X&Y
A + B + C = A|B|C + A&B + A&C + B&C - A&B&C
A + B + C = A&B&C + A|B + A|C + B|C - A|B|C
и после перестановки слагаемых формулы как-то легче запоминаются

Мультик для повторения основных понятий

продолжение... Смотреть всем и зареплять изученное

Самопроверка для крутых информатиков: Решаем и проверяем